Sufficient Reasons
Let $f$ be a Boolean function represented by a random forest $RF$, $x$ be an instance and $1$ (resp. $0$) the prediction of $RF$ on $x$ ($f(x) = 1$ (resp 0)), a sufficient reason for $x$ is a term of the binary representation of the instance that is a prime implicant of $f$ (resp $\neg f$) that covers $x$.
In other words, a sufficient reason for an instance $x$ given a class described by a Boolean function $f$ is a subset $t$ of the characteristics of $x$ that is minimal w.r.t. set inclusion,and such that any instance $x’$ sharing this set t of characteristics is classified by $f$ as $x$ is.
More information about sufficient reasons can be found in the paper Trading Complexity for Sparsity in Random Forest Explanations.
| <Explainer Object>.sufficient_reason(*, time_limit=None): |
|---|
| This method creates a CNF formula corresponding to the negation of the random forest and the instance and then calls a solver (Muser) that extracts a MUS (a Minimum Unsatisfiable Formula) to derive sufficient reasons. Enumerating MUS is a hard task, this is why this function returns only one sufficient reason. Returns a sufficient reason of the current instance. Supports the excluded features. The reason is in the form of binary variables, you must use the to_features method if you want a representation based on the features considered at start. |
time_limit Integer None: The time limit of the method in seconds. Set this to None to give this process an infinite amount of time. Default value is None. |
A sufficient reason is minimal w.r.t. set inclusion, i.e., there is no subset of this reason which is also a sufficient reason. A minimal sufficient reason for $x$ is a sufficient reason for $x$ that contains a minimal number of literals. In other words, a minimal sufficient reason has a minimal size.
| <ExplainerRF Object>.minimal_sufficient_reason(*, time_limit=None): |
|---|
| This method creates a CNF formula corresponding to the negation of the random forest and the instance and next calls a solver (Optilux) that extracts a minimal MUS (Minimum Unsatisfiable Formula) to derive minimal sufficient reasons. Finding one minimal MUS is a hard task, this is the reason why this function allows the extraction of only one minimal sufficient reason. Returns a minimal sufficient reason of the current instance. Supports the excluded features. The reason is in the form of binary variables, you must use the to_features method if you want a representation based on the features considered at start. |
time_limit Integer None: The time limit of the method in seconds. Set this to None to give this process an infinite amount of time. Default value is None. |
The PyXAI library also provides a way to verify that a reason is sufficient:
| <Explainer Object>.is_sufficient_reason(reason, *, n_samples=50): |
|---|
This method checks wheter a reason is sufficient. To this purpose, we first call the method is_reason to check whether n_samples complete binary representations from this reason (randomly generated) lead to the correct prediction or not. Then, we verify the minimality of the reason in the sense of set inclusion. To do that, we delete a literal of the reason, test with is_reason that this new binary representation is not a reason and put back this literal. The method repeats this operation on every literal of the reason. Because this method is based on random generation and a limited number of samples, it is not deterministic and it is not complete (i.e., it is not 100% sure to provide the right answer). Therefore, this method can return True, False or None. |
reason List of Integer: The reason to check. |
n_samples Integer: The number of samples to check, i.e., the number of complete binary representations generated randomly from the reason. Default value is 50. |
Unfortunately, searching for MUS or even more a minimal MUS is a difficult computational task. If the dataset contains a lot of features or if the binary representation of the instance contains many binary variables, finding a MUS may be out of reach. In order to deal with this problem we introduced the notion of Majoritary Reason which is an abductive explanation much easier to compute.
Example from Hand-Crafted Trees
For this example, we take the random forest of the Building Models page consisting of $4$ binary features ($x_1$, $x_2$, $x_3$ and $x_4$).
The following figure shows in red and bold a minimal sufficient reason $(x_1, x_4)$ for the instance $(1,1,1,1)$. 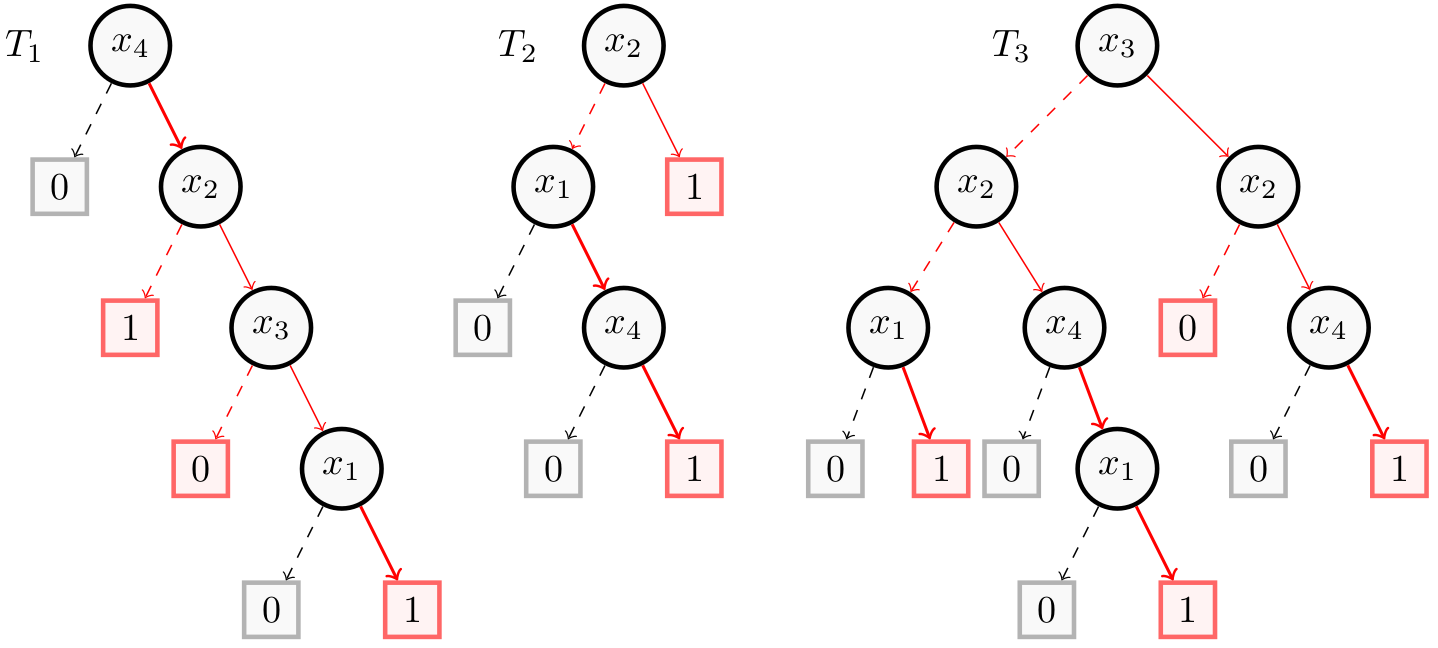
As you can see in the figure, some leaves of this sufficient reason (in red) can have a prediction equal to 0 or 1. These are the predictions from the trees ($T_1$, $T_2$ and $T_3$), but not from the random forest. We need to calculate for each possible interpretation arising from this reason the prediction $f$ from the random forest:
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $T_1$ | $T_2$ | $T_3$ | $f$ |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
As at least 2 trees out of 3 give the right prediction (1), $(x_1, x_4)$ is indeed a sufficient reason.
The next figure shows in blue and bold a minimal sufficient reason $(-x_4)$ for the instance $(0,1,0,0)$. 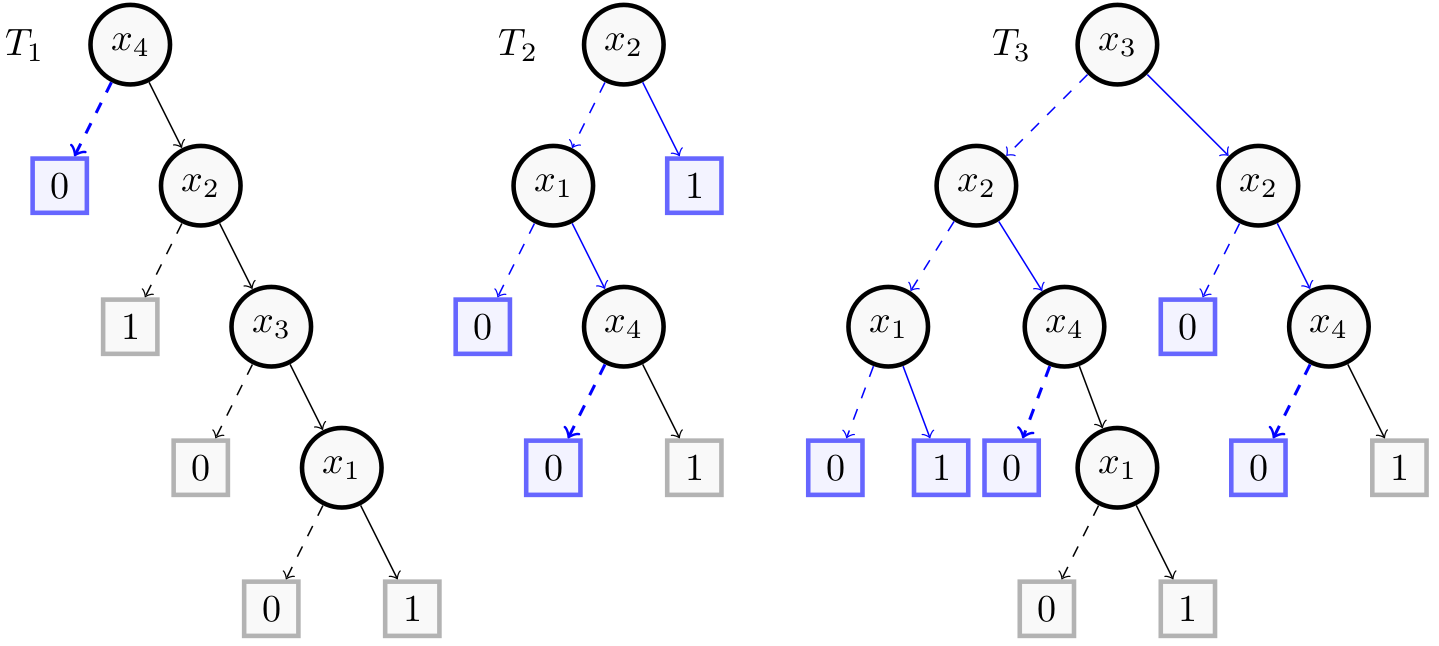
As before, we compute the predictions associated with this reason:
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $T_1$ | $T_2$ | $T_3$ | $f$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
As at least 2 trees out of 3 have the right prediction (0), $(-x_4)$ is indeed a sufficient reason.
Now, we show how to get them with PyXAI. We start by building the random forest:
from pyxai import Builder, Explainer
nodeT1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT1_3 = Builder.DecisionNode(3, left=0, right=nodeT1_1)
nodeT1_2 = Builder.DecisionNode(2, left=1, right=nodeT1_3)
nodeT1_4 = Builder.DecisionNode(4, left=0, right=nodeT1_2)
tree1 = Builder.DecisionTree(4, nodeT1_4, force_features_equal_to_binaries=True)
nodeT2_4 = Builder.DecisionNode(4, left=0, right=1)
nodeT2_1 = Builder.DecisionNode(1, left=0, right=nodeT2_4)
nodeT2_2 = Builder.DecisionNode(2, left=nodeT2_1, right=1)
tree2 = Builder.DecisionTree(4, nodeT2_2, force_features_equal_to_binaries=True) #4 features but only 3 used
nodeT3_1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_1_2 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_4_1 = Builder.DecisionNode(4, left=0, right=nodeT3_1_1)
nodeT3_4_2 = Builder.DecisionNode(4, left=0, right=1)
nodeT3_2_1 = Builder.DecisionNode(2, left=nodeT3_1_2, right=nodeT3_4_1)
nodeT3_2_2 = Builder.DecisionNode(2, left=0, right=nodeT3_4_2)
nodeT3_3_1 = Builder.DecisionNode(3, left=nodeT3_2_1, right=nodeT3_2_2)
tree3 = Builder.DecisionTree(4, nodeT3_3_1, force_features_equal_to_binaries=True)
forest = Builder.RandomForest([tree1, tree2, tree3], n_classes=2)
Then we compute a sufficient reasons for each of these two instances:
explainer = Explainer.initialize(forest)
explainer.set_instance((1,1,1,1))
sufficient = explainer.sufficient_reason()
assert explainer.is_sufficient_reason(sufficient)
assert sufficient == (1, 4), "The sufficient reason is not good !"
minimal = explainer.minimal_sufficient_reason()
print("minimal:", minimal)
assert minimal == (1, 4), "The minimal sufficient reason is not good !"
print("-------------------------------")
instance = (0,1,0,0)
explainer.set_instance(instance)
print("target_prediction:", explainer.target_prediction)
sufficient = explainer.sufficient_reason()
print("sufficient:", sufficient)
assert sufficient == (-1, -3), "The sufficient reason is not good !"
minimal = explainer.minimal_sufficient_reason()
print("minimal:", minimal)
assert minimal == (-4, ), "The minimal sufficient reason is not good !"
minimal: (1, 4)
-------------------------------
target_prediction: 0
sufficient: (-1, -3)
minimal: (-4,)
Example from a Real dataset
For this example, we take the compas dataset. We create a model using the hold-out approach (by default, the test size is set to 30%) and select a well-classified instance.
from pyxai import Learning, Explainer
learner = Learning.Scikitlearn("../../../dataset/compas.csv", learner_type=Learning.CLASSIFICATION)
model = learner.evaluate(method=Learning.HOLD_OUT, output=Learning.RF)
instance, prediction = learner.get_instances(model, n=1, correct=True)
data:
Number_of_Priors score_factor Age_Above_FourtyFive \
0 0 0 1
1 0 0 0
2 4 0 0
3 0 0 0
4 14 1 0
... ... ... ...
6167 0 1 0
6168 0 0 0
6169 0 0 1
6170 3 0 0
6171 2 0 0
Age_Below_TwentyFive African_American Asian Hispanic \
0 0 0 0 0
1 0 1 0 0
2 1 1 0 0
3 0 0 0 0
4 0 0 0 0
... ... ... ... ...
6167 1 1 0 0
6168 1 1 0 0
6169 0 0 0 0
6170 0 1 0 0
6171 1 0 0 1
Native_American Other Female Misdemeanor Two_yr_Recidivism
0 0 1 0 0 0
1 0 0 0 0 1
2 0 0 0 0 1
3 0 1 0 1 0
4 0 0 0 0 1
... ... ... ... ... ...
6167 0 0 0 0 0
6168 0 0 0 0 0
6169 0 1 0 0 0
6170 0 0 1 1 0
6171 0 0 1 0 1
[6172 rows x 12 columns]
-------------- Information ---------------
Dataset name: ../../../dataset/compas.csv
nFeatures (nAttributes, with the labels): 12
nInstances (nObservations): 6172
nLabels: 2
--------------- Evaluation ---------------
method: HoldOut
output: RF
learner_type: Classification
learner_options: {'max_depth': None, 'random_state': 0}
--------- Evaluation Information ---------
For the evaluation number 0:
metrics:
accuracy: 65.71274298056156
nTraining instances: 4320
nTest instances: 1852
--------------- Explainer ----------------
For the evaluation number 0:
**Random Forest Model**
nClasses: 2
nTrees: 100
nVariables: 68
--------------- Instances ----------------
number of instances selected: 1
----------------------------------------------
This dataset is not very large and the computation of a sufficient reason is quite easy, but it is not so easy to derive a minimal one. Since the related solver (Optux) does not propose a time limit mode we commented the related code.
explainer = Explainer.initialize(model, instance)
print("instance:", instance)
print("prediction:", prediction)
print()
sufficient_reason = explainer.sufficient_reason()
print("\nsufficient reason:", sufficient_reason)
print("to features", explainer.to_features(sufficient_reason))
print("is sufficient_reason (for max 50 checks): ", explainer.is_sufficient_reason(sufficient_reason, n_samples=50))
print()
instance: [0 0 1 0 0 0 0 0 1 0 0]
prediction: 0
sufficient reason: (-1, -2, -3, -6, -11, -14)
to features ('Number_of_Priors <= 0.5', 'score_factor <= 0.5', 'Age_Below_TwentyFive <= 0.5', 'African_American <= 0.5')
is sufficient_reason (for max 50 checks): None
Other types of explanations are presented in the Explanations Computation page.