PyXAI

Building Random Forests

This page shows how to build a Random Forest with tree elements (nodes and leaves). To illustrate it, we take an example from the Trading Complexity for Sparsity in Random Forest Explanations paper for recognizing Cattleya orchids.

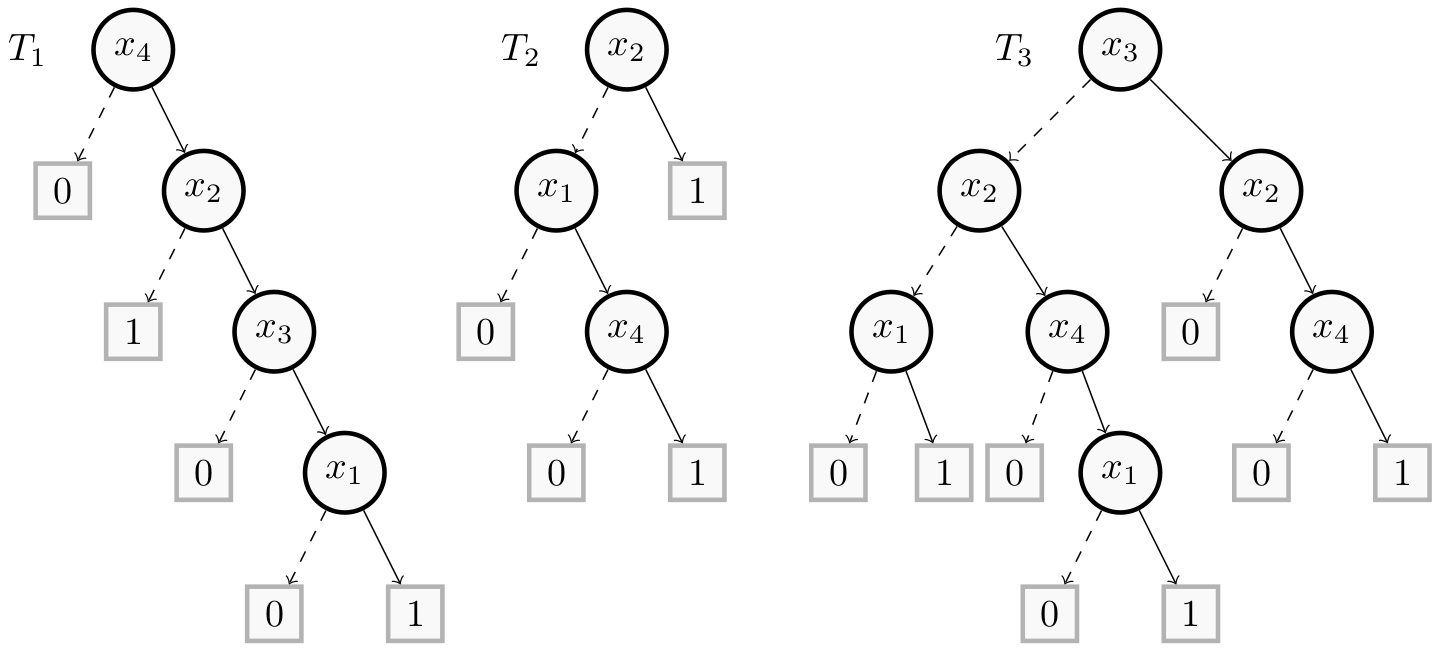
RFbase

The Random Forest (composed of three trees) represented by this figure separates Cattleya orchids from other orchids using the following features:

$x_1$: has fragrant flowers.
$x_2$: has one or two leaves.
$x_3$: has large flowers.
$x_4$: is sympodial.

When a leaf is equal to $1$, the instance is a Cattleya orchid, otherwise it is considered as being from another species.

Building the Model

First, we need to import some modules. Let us recall that the builder module contains methods to build the Decision Tree while the explainer module provides methods to explain it.

from pyxai import Builder, Explainer

Next, we build the tree in a bottom-up way, that is, from the leaves to the root. So we start with $x_1$ node of the first tree $T_1$.

nodeT1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT1_3 = Builder.DecisionNode(3, left=0, right=nodeT1_1)
nodeT1_2 = Builder.DecisionNode(2, left=1, right=nodeT1_3)
nodeT1_4 = Builder.DecisionNode(4, left=0, right=nodeT1_2)

tree1 = Builder.DecisionTree(4, nodeT1_4, force_features_equal_to_binaries=True)

In this example, as each feature is binary (i.e. takes for value either 0 or 1), we do not include in the Builder.DecisionNode class the operator and the threshold parameters. Thus, the values of these parameters are those by default (respectively, OperatorCondition.GE and $0.5$). This gives us conditions for each node of the form “$x_i \ge 0.5$ ?”. In the Boosted Tree page, more complex conditions are created.

Next, we build the tree $T_2$:

nodeT2_4 = Builder.DecisionNode(4, left=0, right=1)
nodeT2_1 = Builder.DecisionNode(1, left=0, right=nodeT2_4)
nodeT2_2 = Builder.DecisionNode(2, left=nodeT2_1, right=1)

tree2 = Builder.DecisionTree(4, nodeT2_2, force_features_equal_to_binaries=True) #4 features but only 3 used

The first parameter (n_features) of the Builder.DecitionTree method is set to 4 in this tree, even if there are only 3 features used. Indeed, it is necessary to consider the total number of features used by all trees of the model (not only those of this specific Decision Tree).

And the tree $T_3$:

nodeT3_1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_1_2 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_4_1 = Builder.DecisionNode(4, left=0, right=nodeT3_1_1)
nodeT3_4_2 = Builder.DecisionNode(4, left=0, right=1)

nodeT3_2_1 = Builder.DecisionNode(2, left=nodeT3_1_2, right=nodeT3_4_1)
nodeT3_2_2 = Builder.DecisionNode(2, left=0, right=nodeT3_4_2)

nodeT3_3_1 = Builder.DecisionNode(3, left=nodeT3_2_1, right=nodeT3_2_2)

tree3 = Builder.DecisionTree(4, nodeT3_3_1, force_features_equal_to_binaries=True)

The parameter force_features_equal_to_binaries allows one to make binary variables equal to feature identifiers. These binary variables are used to represent explanations. Their values and signs indicate whether the conditions of nodes are satisfied or not. By default, these binary variables have random values depending on the order with the tree is traversed. Setting the parameter force_features_equal_to_binaries to True ensures that the binary variables no longer receive random values. This allows us to have explanations that match the features, without having to use the to_features method. However, this functionality cannot be used with all models because it is not compatible when nodes have different conditions on the same feature. It assumes that the features are the conditions.

We can now define the Random Forest:

forest = Builder.RandomForest([tree1, tree2, tree3], n_classes=2)

More details about the DecisionNode and RandomForest classes are given in the Building Models page.

Explaining the Model

Let us compute explanations. Let us start with the instance (1,1,1,1):

print("For instance = (1,1,1,1):")
print("")
instance = (1,1,1,1)
explainer = Explainer.initialize(forest, instance=instance)
print("target_prediction:", explainer.target_prediction)

direct = explainer.direct_reason()
print("direct:", direct)
assert direct == (1, 2, 3, 4), "The direct reason is not good !"

sufficient = explainer.sufficient_reason()
print("sufficient:", sufficient)
assert sufficient == (1, 4), "The sufficient reason is not good !"

minimal = explainer.minimal_sufficient_reason()
print("minimal:", minimal)
assert minimal == (1, 4), "The minimal reason is not good !"

majoritary = explainer.majoritary_reason()
print("majoritary:", majoritary)

minimal_contrastives = explainer.minimal_contrastive_reason(n=Explainer.ALL)
print("minimal_contrastive: ", minimal_contrastives)

minimals = explainer.preferred_majoritary_reason(method=Explainer.MINIMAL, n=10)
print("minimals:", minimals)

for c in minimal_contrastives:
  assert explainer.is_contrastive_reason(c), "..."

For instance = (1,1,1,1):

target_prediction: 1
direct: (1, 2, 3, 4)
sufficient: (1, 4)
minimal: (1, 4)
majoritary: (1, 2, 4)
minimal_contrastive:  ((4,),)
minimals: ((2, 3, 4), (1, 3, 4), (1, 2, 4))

And now with the instance (0,0,0,0):

print("\nFor instance = (0,1,0,0):")
print("")
instance = (0,1,0,0)
explainer.set_instance(instance=instance)
print("target_prediction:", explainer.target_prediction)

direct = explainer.direct_reason()
print("direct:", direct)
assert direct == (2, -3, -4), "The direct reason is not good !"

sufficient = explainer.sufficient_reason()
print("sufficient:", sufficient)
assert sufficient == (-1, -3), "The sufficient reason is not good !"

minimal = explainer.minimal_sufficient_reason()
print("minimal:", minimal)
assert minimal == (-4, ), "The minimal reason is not good !" 

majoritary = explainer.majoritary_reason(n=Explainer.ALL)
print("majoritary:", majoritary)

minimals = explainer.preferred_majoritary_reason(method=Explainer.MINIMAL, n=10)
print("minimals:", minimals)

minimal_contrastives = explainer.minimal_contrastive_reason(n=Explainer.ALL)
print("minimal_contrastive: ", minimal_contrastives)

for c in minimal_contrastives:
  assert explainer.is_contrastive_reason(c), "..."

For instance = (0,1,0,0):

target_prediction: 0
direct: (2, -3, -4)
sufficient: (-1, -3)
minimal: (-4,)
majoritary: ((2, -4), (-1, -4), (-1, 2, -3))
minimals: ((2, -4), (-1, -4))
minimal_contrastive:  ((-3, -4), (-1, -4))

Details on explanations are given in the Explanations Computation page.