Contrastive Reasons
The algorithms to compute contrastive reasons for multi-class classification problems are still under development and should be available in the next versions of PyXAI (however, the contrastive reasons for binary classification can be calculated).
Unlike abductive explanations that explain why an instance $x$ is classified as belonging to a given class, the contrastive explanations explains why $x$ has not been classified by the ML model as expected.
Let 𝑓 be a Boolean function represented by a random forest 𝑅𝐹, 𝑥 be an instance and 1 (resp. 0) the prediction of 𝑅𝐹 on 𝑥 (𝑓(𝑥)=1 (resp $f(x)=0$)), a contrastive reason for $x$ is a term $t$ such that:
- $t \subseteq t_{x}$, $t_{x} \setminus t$ is not an implicant of $f;$
- for every $\ell \in t$, $t \setminus {\ell}$ does not satisfy this previous condition (i.e., $t$ is minimal w.r.t. set inclusion).
Formally, a contrastive reason for $x$ is a subset $t$ of the characteristics of $x$ that is minimal w.r.t. set inclusion among those such that at least one instance $x’$ that coincides with $x$ except on the characteristics from $t$ is not classified by the decision tree as $x$ is. Stated otherwhise, a contrastive reason represents adjustments of the features that we have to do to change the prediction for an instance.
A contrastive reason is minimal w.r.t. set inclusion, i.e. there is no subset of this reason which is also a contrastive reason. A minimal contrastive reason for $x$ is a contrastive reason for $x$ that contains a minimal number of literals. In other words, a minimal contrastive reason has a minimal size.
More information about contrastive reasons can be found in the paper On the Explanatory Power of Decision Trees.
For random forests, PyXAI can only compute minimal contrastive reasons.
| <ExplainerRF Object>.minimal_contrastive_reason(*, n=1, time_limit=None): |
|---|
| This method considers a CNF formula corresponding to the negation of the random forest as hard clauses and adds binary variables representing the instances as unary soft clauses with weights equal to 1. Several calls to a MAXSAT solver (OPENWBO) are performed and the result of each call is a minimal contrastive reason. The minimal reasons are those with the lowest scores (i.e., the sum of weights). Thus, the algorithm stops its search when a non-minimal reason is found (i.e., when a higher score is found). Moreover, the method prevents from finding the same reason twice or more by adding clauses(called blocking clauses) between each invocation. Return n minimal contrastive reasons of the current instance in a Tuple (when n is set to 1, does not return a Tuple but just the reason). Supports the excluded features. The reasons are in the form of binary variables, you must use the to_features method if you want a representation based on the features considered at start. |
n Integer Explainer.ALL: The desired number of contrastive reasons. Set this to Explainer.ALL to request all reasons. Default value is 1. |
time_limit Integer None: The time limit of the method in seconds. Set this to None to give this process an infinite amount of time. Default value is None. |
The PyXAI library provides a way to check that a reason is contrastive:
| <Explainer Object>.is_contrastive_reason(reason): |
|---|
Checks if the reason is a contrastive one. Replaces in the binary representation of the instance each literal of the reason with its opposite and checks that the result does not predict the same class as the initial instance. Returns True if the reason is contrastive, False otherwise. |
reason List of Integer: The reason to be checked. |
The basic methods (initialize, set_instance, to_features, is_reason, …) of the Explainer module used in the next examples are described in the Explainer Principles page.
Example from Hand-Crafted Trees
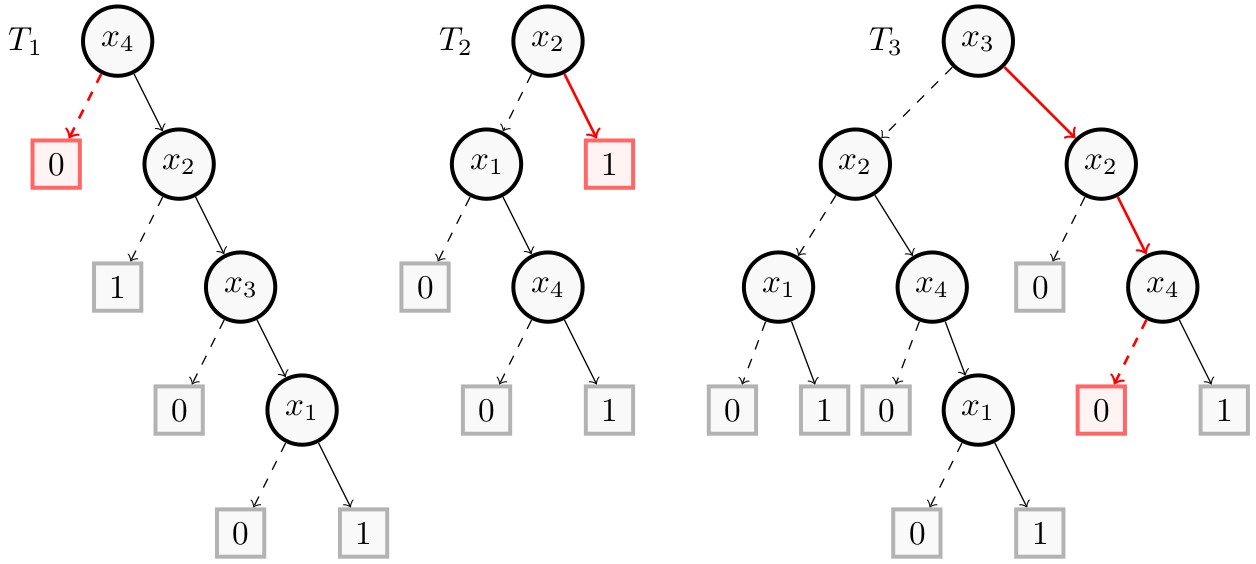
For this example, we take the random forest of the Building Models page consisting of $4$ binary features ($x_1$, $x_2$, $x_3$ and $x_4$).
The following figure shows the new instance $x’ = (1,1,1,0)$ created from the contrastive reason $(x_4)$ in red for the instance $x = (1,1,1,1)$. Thus, the instance $(1,1,1,0)$ that differs with $x$ only on $x_4$ is not classified by $T$ as $x$ is. More precisely, $x’$ is classified as a negative instance while $x$ is classified as a positive instance. Indeed, in this figure, $T_1(x’) = 0$, $T_2(x’) = 1$ and $T_3(x’) = 0$, so $f(x’) = 0$.
Now, we show how to get them with PyXAI. We start by building the random forest:
from pyxai import Builder, Explainer
nodeT1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT1_3 = Builder.DecisionNode(3, left=0, right=nodeT1_1)
nodeT1_2 = Builder.DecisionNode(2, left=1, right=nodeT1_3)
nodeT1_4 = Builder.DecisionNode(4, left=0, right=nodeT1_2)
tree1 = Builder.DecisionTree(4, nodeT1_4, force_features_equal_to_binaries=True)
nodeT2_4 = Builder.DecisionNode(4, left=0, right=1)
nodeT2_1 = Builder.DecisionNode(1, left=0, right=nodeT2_4)
nodeT2_2 = Builder.DecisionNode(2, left=nodeT2_1, right=1)
tree2 = Builder.DecisionTree(4, nodeT2_2, force_features_equal_to_binaries=True) #4 features but only 3 used
nodeT3_1_1 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_1_2 = Builder.DecisionNode(1, left=0, right=1)
nodeT3_4_1 = Builder.DecisionNode(4, left=0, right=nodeT3_1_1)
nodeT3_4_2 = Builder.DecisionNode(4, left=0, right=1)
nodeT3_2_1 = Builder.DecisionNode(2, left=nodeT3_1_2, right=nodeT3_4_1)
nodeT3_2_2 = Builder.DecisionNode(2, left=0, right=nodeT3_4_2)
nodeT3_3_1 = Builder.DecisionNode(3, left=nodeT3_2_1, right=nodeT3_2_2)
tree3 = Builder.DecisionTree(4, nodeT3_3_1, force_features_equal_to_binaries=True)
forest = Builder.RandomForest([tree1, tree2, tree3], n_classes=2)
We compute the contrastive reasons for these two instances:
explainer = Explainer.initialize(forest)
explainer.set_instance((1,1,1,1))
contrastives = explainer.minimal_contrastive_reason(n=Explainer.ALL)
print("Contrastives:", contrastives)
for contrastive in contrastives:
assert explainer.is_contrastive_reason(contrastive), "It is not a contrastive reason !"
print("-------------------------------")
explainer.set_instance((0,0,0,0))
contrastives = explainer.minimal_contrastive_reason(n=Explainer.ALL)
print("Contrastives:", contrastives)
for contrastive in contrastives:
assert explainer.is_contrastive_reason(contrastive), "It is not a contrastive reason !"
Contrastives: ((4,),)
-------------------------------
Contrastives: ((-1, -4),)
Example from a Real Dataset
For this example, we take the mnist49 dataset. We create a model using the hold-out approach (by default, the test size is set to 30%) and select a well-classified instance.
from pyxai import Learning, Explainer
learner = Learning.Scikitlearn("../../../dataset/mnist49.csv", learner_type=Learning.CLASSIFICATION)
model = learner.evaluate(method=Learning.HOLD_OUT, output=Learning.RF)
instance, prediction = learner.get_instances(model, n=1, correct=True)
data:
0 1 2 3 4 5 6 7 8 9 ... 775 776 777 778 779 780 781
0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 \
1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
... .. .. .. .. .. .. .. .. .. .. ... ... ... ... ... ... ... ...
13777 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
13778 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
13779 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
13780 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
13781 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
782 783 784
0 0 0 4
1 0 0 9
2 0 0 4
3 0 0 9
4 0 0 4
... ... ... ...
13777 0 0 4
13778 0 0 4
13779 0 0 4
13780 0 0 9
13781 0 0 4
[13782 rows x 785 columns]
-------------- Information ---------------
Dataset name: ../../../dataset/mnist49.csv
nFeatures (nAttributes, with the labels): 785
nInstances (nObservations): 13782
nLabels: 2
--------------- Evaluation ---------------
method: HoldOut
output: RF
learner_type: Classification
learner_options: {'max_depth': None, 'random_state': 0}
--------- Evaluation Information ---------
For the evaluation number 0:
metrics:
accuracy: 98.21039903264813
nTraining instances: 9647
nTest instances: 4135
--------------- Explainer ----------------
For the evaluation number 0:
**Random Forest Model**
nClasses: 2
nTrees: 100
nVariables: 27880
--------------- Instances ----------------
number of instances selected: 1
----------------------------------------------
We compute one contrastive reason. Since it is a hard task, we put a time_limit. If time_limit is reached, we obtain either an approximation of a contrastive reason (some literals can be redundant) or the empty list if no contrastive reason was found:
explainer = Explainer.initialize(model, instance)
print("instance prediction:", prediction)
print()
contrastive_reason = explainer.minimal_contrastive_reason(n=1, time_limit=10)
if explainer.elapsed_time == Explainer.TIMEOUT:
print('this is an approximation')
if len(contrastive_reason) > 0:
print("constrative: ", explainer.to_features(contrastive_reason, contrastive=True))
else:
print('No contrative reason found')
instance prediction: 0
this is an approximation
constrative: ('153 <= 127.5', '154 <= 104.5', '155 <= 127.0', '157 <= 2.5', '158 <= 0.5', '161 > 0.5', '162 > 0.5', '182 <= 12.5', '183 <= 253.5', '184 <= 10.5', '186 <= 101.0', '188 > 17.5', '189 > 3.5', '192 <= 0.5', '208 <= 163.5', '209 <= 1.5', '210 <= 162.0', '211 <= 49.0', '212 <= 254.5', '213 <= 5.0', '216 > 3.5', '232 <= 1.0', '235 <= 5.0', '236 <= 252.5', '237 <= 26.5', '239 <= 36.5', '240 <= 6.0', '241 <= 40.5', '243 > 7.5', '244 > 110.5', '266 <= 212.5', '267 <= 249.5', '269 <= 0.5', '289 <= 254.5', '291 <= 0.5', '292 <= 253.5', '295 <= 6.5', '319 <= 246.0', '320 <= 125.0', '321 <= 253.5', '322 <= 253.5', '326 <= 253.5', '328 > 2.5', '382 > 193.5', '399 <= 1.0', '400 <= 2.0', '428 > 19.5', '429 > 21.5', '435 > 24.5', '454 > 0.5', '456 > 4.5', '465 <= 248.5', '469 <= 0.5', '545 <= 254.5', '550 > 6.5', '592 <= 14.0', '612 <= 2.5', '621 <= 88.0', '633 <= 252.5', '688 <= 253.5', '706 <= 77.5', '711 <= 6.5', '712 <= 1.5', '717 <= 18.5', '735 <= 2.0', '745 <= 25.5', '746 <= 21.5', '750 <= 8.5', '770 <= 19.5')
Other types of explanations are presented in the Explanations Computation page.