Boosted Tree Explanations
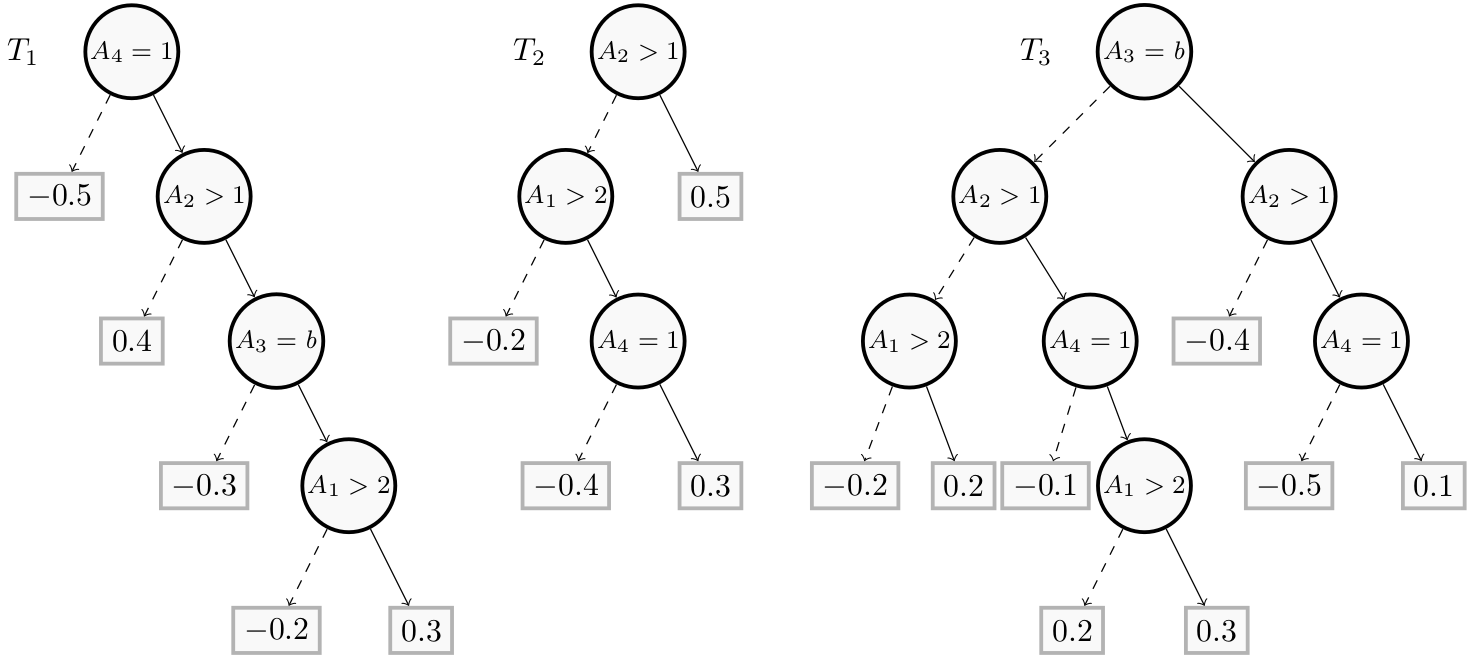
Contrary to a decision tree (where the leaves represent classes), a regression tree is a binary tree $T$ where the leaves represent numerical values $w_i \in \mathbb{R}$ that describe real quantities.
A forest $F$ associated with a class $j$ is an ensemble of trees {$T_1,\ldots T_n$} where each $T_n^j$ is a regression tree such that the weight $W(F, x) \in \mathbb{R}$ for an input instance $x$ is given by:
\[W(F, x) = \sum_{i=1}^{n} w(T_i, x)\]where the weight $w(T_i, x) \in \mathbb{R}$ of a tree $T_i$ for an input instance $x$ is given by the label of the leaf reached from the root as follows: at each node go to the left or right child depending on whether or not the condition labeling the node is satisfied by $x$.
In our context, the prediction computation of a gradient boosted tree classifier is realized differently depending on the number of classes included in the dataset.
- In a binary classification case, a boosted tree $BT$ consists of only one forest $F = {T_1,\cdots,T_{n}}$ and an instance $x$ is considered as a positive instance when $W(F,x) > 0$ and as a negative instance otherwise. We note $BT(x) = 1$ in the first case and $BT(x) = 0$ in the second case.
- In a multi-class context, a boosted tree $BT$ is a collection of $m$ forests $BT = {F^1,\ldots, F^m}$ where each forest is associated with a class $C_j$ and an instance $x$ is classified as an element of class $C_j$, noted $BT(x) = j$, if and only if $W(F^j, x) > W(F^i, x)$ for every class $C_i$ such $i \neq j$.
For boosted trees classifiers, PyXAI supports both binary and multi-class classification explanations.