Sufficient Reasons
Formally, an abductive explanation $t$ for an instance $x$ given a classifier $f$ (that is binary or not) is a subset $t$ of the characteristics of $x$ such that every instance $x’$ sharing this set t of characteristics is classified by $f$ as $x$ is. A sufficient reason $t$ for $x$ given $f$ is an abductive explanation for $x$ given $f$ such that no proper subset $t’$ of $t$ is an abductive explanation for $x$ given $f$ (i.e., minimal w.r.t. set inclusion).
Considering the boosted tree of the Building Models page consisting of $4$ features ($A_1$, $A_2$, $A_3$ and $A_4$), we can derive as an example the sufficient reason $t$ = ($A_1 = 4$, $A_4 = 1$) for the instance $x$ = ($A_1=4$, $A_2 = 3$, $A_3 = 1$, $A_4 = 1$). In this figure, this sufficient reason is shown in red:
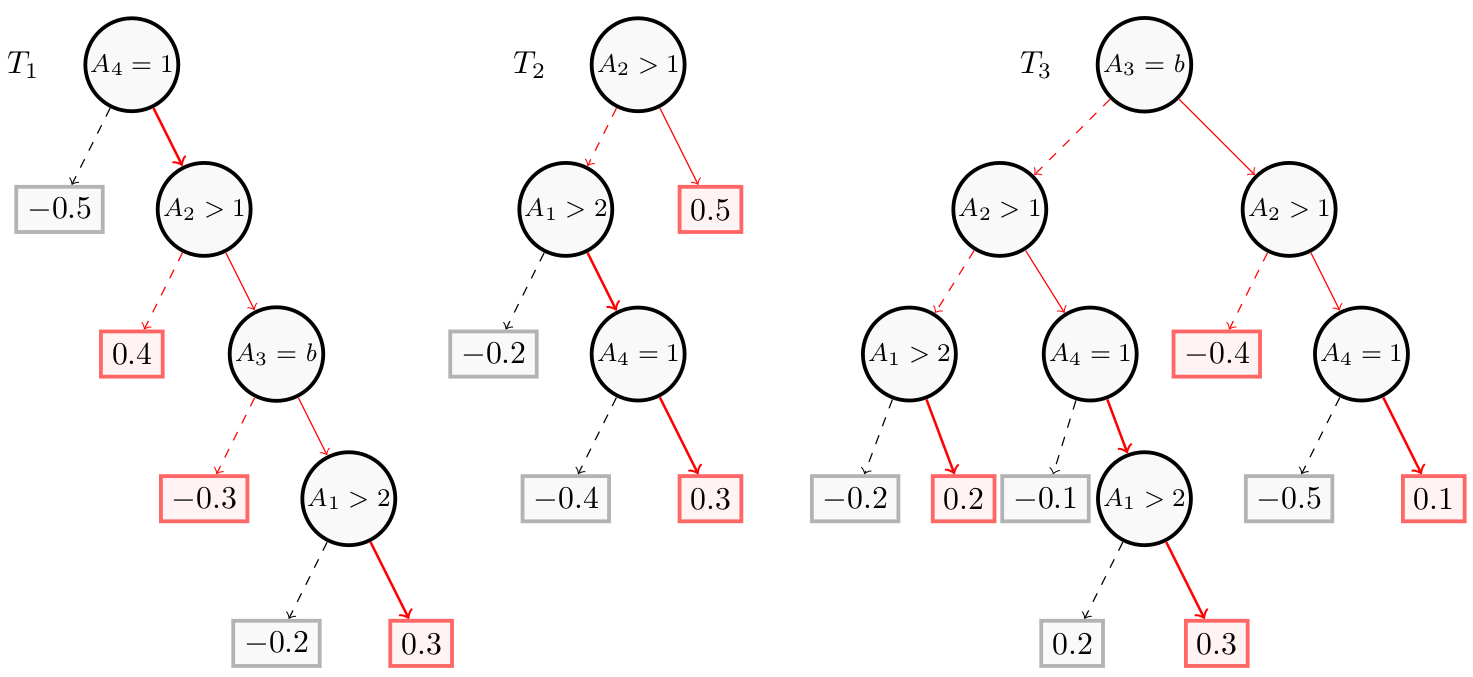
As you can see on the figure, some leaves of this sufficient reason corresponds to positive or negative predictions. However, all the instances $x’$ extending $t$ can be gathered into four categories, obtained by considering the truth values of the Boolean conditions over the two remaining attributes ($A_2$ and $A_3$) as encountered in the trees of $BT$. This table shows that, in every case, we have $W(F, x’) > 0$, showing that $f(x’) = 1$.
| $A_1 = 4$ | $A_2 = 3$ | $A_3 = 1$ | $A_4 = 4$ | $w(T_1,x')$ | $w(T_2,x')$ | $w(T_3,x')$ | $W(F,x)$ |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0.4 | 0.3 | 0.2 | 0.9 |
| 1 | 0 | 1 | 1 | 0.4 | 0.3 | -0.4 | 0.3 |
| 1 | 1 | 0 | 1 | -0.3 | 0.5 | 0.3 | 0.5 |
| 1 | 1 | 1 | 1 | 0.3 | 0.5 | 0.1 | 0.9 |
The algorithms to compute sufficient reasons are still under development and should be available in the next versions of PyXAI.
Calculating the sufficient reasons is a computationally difficult task (deciding whether $t$ is an abductive explanation for $x$ given $BT$ is ${\sf coNP}$-complete. To overcome this problem, we introduce another kind of abductive explanations easier to calculate, the Tree-Specific reasons.