XCSP3
Nonograms are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers to the left and at the top of the grid to reveal a hidden picture.
In this type of puzzle, the numbers are a form of discrete tomography that gives the number and the length of groups of consecutive painted cells for each line and for each column.
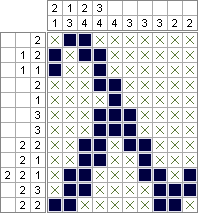

How to represent this
problem using XCSP3?
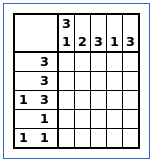
Step 1: Variables
Each cell in the 5 x 5 nonogram is encoded with a 0,1 variable.
Accordingly, an array 5 x 5 of {0,1} is introduced:
<variables>
<array id="x" size="[5][5]"> 0..1 </array>
</variables>
For instance,
x[2,3]=1 expresses that the cell in line #2 col #3 is colored.
x[2,3]=0 expresses that the cell in line #2 col #3 is left blank.
Step 2: Constraints
The patterns that form the expected solution of the puzzle is encoded through a so-called regular constraint.
The regular constraint ensures that the sequence of values assigned to the variables it involves forms a word that can be recognized by a (possibly non-)deterministic finite automaton.
The scope of the constraint is given by the element list, and three elements, transitions, start and final, are introduced for representing respectively the transitions, the start state and the final states of the automaton.
Let us represent the pattern expected in the first line (line #0) of our example:
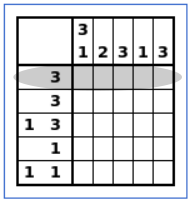
It forces the line to contain a group of 3 consecutive colored squares.
In other words, the (0,1) word formed by this line must follow this automaton:
With XCSP3, this is translated by the following constraint:
<regular>
<list> x[0][] </list>
<transitions>
(a,0,a) (a,1,b) (b,1,c) (c,1,d) (d,0,d)
</transitions>
<start> a </start>
<final> d </final>
</regular>
Gathering constraints
The same constraint (a group of 3 consecutive colored cells) also exists for line #1 and for columns #2 and #4
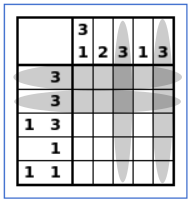
XCSP3 allows us to factorize constraints that appear with the same constraint expression and different parameters, thanks to the group and args elements.
<group>
<regular>
<list> %... </list>
<transitions>
(a,0,a) (a,1,b) (b,1,c) (c,1,d) (d,0,d)
</transitions>
<start> 0 </start>
<final> 1 </final>
</regular>
<args> x[0][] </args>
<args> x[1][] </args>
<args> x[][2] </args>
<args> x[][4] </args>
</group>This is it!
The same thing has to be done for each line/column of the grid, and our nonogram is now represented with XCSP3.
Full XCSP3 representation:
<instance format="XCSP3" type="CSP">
<variables>
<array id="x" size="[5][5]"> 0..1 </array>
</variables>
<constraints>
<group>
<regular>
<list> %... </list>
<transitions>
(a,0,a) (a,1,b) (b,1,c) (c,1,d) (d,0,d)
</transitions>
<start> a </start>
<final> d </final>
</regular>
<args> x[0][] </args>
<args> x[1][] </args>
<args> x[][2] </args>
<args> x[][4] </args>
</group>
<group>
<regular>
<list> %... </list>
<transitions>
(a,0,a) (a,1,b) (b,0,b)
</transitions>
<start> a </start>
<final> b </final>
</regular>
<args> x[3][] </args>
<args> x[][3] </args>
</group> <regular>
<list> x[2][] </list>
<transitions>
(a,0,a) (a,1,b) (b,0,c) (c,0,c)
(c,1,d) (d,1,e) (e,1,f) (f,0,f)
</transitions>
<start> a </start> <final> f </final>
</regular>
<regular>
<list> x[4][] </list>
<transitions>
(a,0,a) (a,1,b) (b,0,c) (c,0,c) (c,1,d) (d,0,d)
</transitions>
<start> a </start> <final> d </final>
</regular>
<regular>
<list> x[][0] </list>
<transitions>
(a,0,a) (a,1,b) (b,1,c) (c,1,d)
(d,0,e) (e,0,e) (e,1,f) (f,0,f)
</transitions>
<start> a </start> <final> f </final>
</regular>
<regular>
<list> x[][1] </list>
<transitions>
(a,0,a) (a,1,b) (b,1,c) (c,0,c)
</transitions>
<start> a </start> <final> d </final>
</regular>
</constraints>
</instance>
For full specifications of XCSP3, examples and benchmarks,
visit XCSP3 home page