Pseudo-Boolean Competition 2009: requirements for solvers
This document lists the requirements that a solver
must conform to. These requirements may evolve slightly over time.
You're invited to check the content of this page regularly. The
revisions of this document are detailed below.
Last modification: 2008-11-25 (YYYY-MM-DD format)
Revisions of this document
Major
Minor
Registering the solver to the right category
Because not all solvers are able to solve every kind of instances, you
will be asked when you register your solver to indicate which category
of benchmarks it is able to handle. This year, we have up to 8
categories defined by the ability of the solver to
- deal with an optimization function or not,
- deal with linear or non linear constraints,
- deal with small or big integers
Two categories are defined based on the presence of an objective
function or not:
- Category DEC (decision problem)
Benchmarks in this category do not contain an objective function.
The solver is expected to answer SATISFIABLE or UNSATISFIABLE. All
solvers should register in this category. This category was called SAT/UNSAT in the previous evaluations.
- Category OPT (optimisation problem)
Benchmarks in this category contain an objective function which should
be minimized. Solvers entering this category must be able to find the
best solution and give an OPTIMUM FOUND answer.
Two categories are defined based on the kind of contraints contained in
the instance:
- Category "linear constraints" (LIN)
All contraints in the instance are linear pseudo-Boolean constraints.
All solvers should register in this category.
- Category "non linear constraints" (NLC)
At least one constraint (or the objective function) is non linear,
meaning that it contains at
least one product of Boolean variables. A non linear constraint or
objective function can
always be linearized by introducing new variables.
As we provide parsers which will automatically perform a basic
linearization, we expect that all solvers will register in this
category. Solvers which do not register in this category will be run a
linearized version of the benchmark using default techniques.
As explained in the section on the input format (see below), benchmarks
may contain arbitrarily long integers that do not fit in a usual
32-bits
integer. The page on integer overflows
explains why we consider that a strong solver should use a multiple
precision integer library. However, we do not require that you modify
your existing solver to use big integers. We just need that you
register your solver in the categories which it is able to solve. This
is an important decision because registering a solver in a given
category is a claim that it will give correct answers for each
benchmark in that category.
Concerning the integers values, two categories are defined
- Category "small integers" (SMALLINT)
Benchmarks in this category contain only small integers, which
means that they contain no constraint with a sum of coefficients
greater than or equal to 221 (each number has up to
20 bits). Solvers which use 32-bits integers are most probably safe,
unless they use some fancy learning scheme. All solvers should register
in this category.
- Category "big integers" (BIGINT)
Benchmarks in this category have at least one constraint
with a sum of coefficients greater than or equal to 221 (at
least 21 bits). Only solvers with support for big integers should
register in this category.
Complete and incomplete solvers
Complete solvers are solvers which can always decide if the formula is
satisfiable or not, provided they are given enough time and memory.
Incomplete solvers are able to give some answers (SAT/UNSAT) but not
all. They may loop endlessly in a number of cases. Local search
algorithms are examples of incomplete solvers. There is a high
probability that they find a solution if the instance is satisfiable,
but they will not be able to prove unsatisfiability.
Both kinds of solvers are welcome in this evaluation. Submitters will
have to indicate if their solver is complete or incomplete on
the submission form.
Complete solvers
There is no special requirement about complete solvers. See the input
and output format that all solvers must respect for details.
Incomplete solvers
Incomplete solvers are definitely welcome in this evaluation. Despite
the fact that they will never answer UNSATISFIABLE or OPTIMUM FOUND,
incomplete solvers can be registered in both the DEC and OPT
categories.
In the DEC category, an incomplete solver will stop as soon as it
finds a solution and will time out if it can't find one. The only
difference with a complete solver is that it will time out
systematically on unsatisfiable instances.
In the optimisation category, an incomplete solver will systematically
time out because it will be unable to prove that it has found the
optimum solution. Yet, it may have found the optimum value well before
the time out. In order to get relevant informations in this category,
an incomplete solver must fulfill two requirements:
- it must intercept the SIGTERM sent to the solver on timeout and
output either "s UNKNOWN" or "s SATISFIABLE" with the "v " line
corresponding to the best model it has found
- it MUST output "o " lines whenever it finds a better solution so
that, even if the solver always timeout, the timestamp of the last "o "
line indicates when the best solution was found. Keep in mind that it
is the evaluation environment which is in charge of timestamping "o "
lines.
Execution environment
Solvers will run on a cluster of computers using the Linux operating
system. They will run under the control of another program
(runsolver) which will enforce some limits on the memory and the total
CPU time used by the program.
Solvers will be run inside a sandbox that will prevent unauthorized use
of the system (network connections, file creation outside the allowed
directory, among others).
Solvers can be run as either as 32 bits or 64 bits applications. If you
submit an executable, you are required to provide us with an ELF
executable (preferably statically linked). Authors submitting solvers
in source
form will have to specify if it should be compiled in 32 bits o 64 bits
mode.
Two executions of a solver with the same parameters and system
resources must output the same result in approximately the same time
(so that the experiments can be repeated).
During the submission process, you will be asked to provide the
organizers with a suggested command line that should be used to run
your solver. In this command line, you will be asked to use the
following placeholders, which will be replaced by the actual
informations by the evaluation environment.
- BENCHNAME will be replaced by the name of the file containing the
instance to solve. Obviously, the solver must use this parameter.
- RANDOMSEED will be replaced by a random seed which is a number
between 0 and 4294967295. This parameter MUST be used to initialize the
random number generator when the solver uses random numbers. It is
recorded by the evaluation environment and will allow to run the
program on a given instance under the same conditions if necessary.
- TIMELIMIT (or TIMEOUT) represents the total CPU time (in seconds)
that the
solver may use before being killed. May be used to adapt the solver
strategy.
- MEMLIMIT represents the total amount of memory (in MiB) that the
solver may use
before being killed. May be used to adapt the solver
strategy.
- TMPDIR is the name of the only directory where the solver is
allowed to read/write temporary files
- DIR is the name of the directory where the solver files will be
stored
Examples of command lines:
DIR/mysolver BENCHNAME RANDOMSEED
DIR/mysolver --mem-limit=MEMLIMIT --time-limit=TIMELIMIT --tmpdir=TMPDIR BENCHNAME
java -jar DIR/mysolver.jar -c DIR/mysolver.conf BENCHNAME
As an example, these command lines could be expanded by the
evaluation environment as
/solver10/mysolver /tmp/file.pb 1720968
/solver10/mysolver --mem-limit=900 --time-limit=1200 --tmpdir=/tmp/job12345 /tmp/file.pb
java -jar /solver10/mysolver.jar -c /solver10/mysolver.conf /tmp/file.pb
The command line provided by the submitter is only a suggested command
line. Organizers may have to modify this command line (e.g. memory
limits of the Java Virtual Machine (JVM) may have to be modified to
cope with the actual memory limits).
The solver may also (optionally) use the values of the following
environment variables:
- TIMELIMIT (or TIMEOUT) (the number of seconds it will be allowed
to run)
- MEMLIMIT (the amount of RAM in MiB available to the solver)
- TMPDIR (the absolute pathname of the only directory where the
solver is allowed to create temporary files)
After TIMEOUT seconds have elapsed, the solver will first receive
a SIGTERM to give it a chance to output the best solution it found so
far (in the case of an optimization problem). One second later, the
program will receive a SIGKILL signal from the controlling program to
terminate the solver.
The solver cannot write to any file
except standard output,
standard error and files in the TMPDIR directory. A solver is not
allowed to open any network connection or launch unexpected external
commands. Solvers may use several processes or threads.
Input Format
The input format allows the specification of both linear and
non-linear
pseudo-Boolean instances.
As in the previous evaluations, the input file format for
pseudo-Boolean instances is a variant of the OPB
format (see the end of the README
file in http://www.mpi-sb.mpg.de/units/ag2/software/opbdp/opbdp1.1.1.tar.gz).
For linear pseudo-Boolean instances, the file format is exactly the
same as in the PB06 evaluation. For non-linear pseudo-Boolean
instances, a generalization of this
format
is proposed with the following changes:
- Both in the objective function and in the constraints, the input
format
allows the specification of product of literals. Since literals are
assigned values from {0,1}, a product of literals is interpreted as 1
if and only if all of its literals are assigned to 1. In Boolean
terms, a product represents a conjunction of literals.
- Products contain literals instead of variables.
Therefore, variable names can be preceded with the character '~' in
order to
specify the negative literal of that variable
With these generalizations, it is possible to specify constraints
like:
3 x1 x2 + 2 ~x3 ~x4 ~x5 -3 x6 >= +2 ;
If we would not allow negative literals in the format, we would have to
replace the term
2 ~x3 ~x4 ~x5
with the following expression
-2 x3 -2 x4 -2 x5 +2 x3 x4 +2 x3 x5 +2 x4 x5 -2 x3 x4 x5 +2
Here are a few examples:
Linear
instances
|
Non-linear
instances
|
* #variable= 5 #constraint= 4
*
* this is a dummy instance
*
min: 1 x2 -1 x3 ;
1 x1 +4 x2 -2 x5 >= 2;
-1 x1 +4 x2 -2 x5 >= +3;
12345678901234567890 x4 +4 x3 >= 10;
* an equality constraint
2 x2 +3 x4 +2 x1 +3 x5 = 5;
|
* #variable= 5 #constraint= 4 #product= 5 sizeproduct= 13
*
* this is a dummy instance
*
min: 1 x2 x3 -1 x3 ;
1 x1 +4 x1 ~x2 -2 x5 >=2;
-1 x1 +4 x2 -2 x5 >= 3;
12345678901234567890 x4 +4 x3 >= 10;
2 x2 x3 +3 x4 ~x5 +2 ~x1 x2 +3 ~x1 x2 x3 ~x4 ~x5 = 5 ;
|
* #variable= 15
#constraint= 21
*
* linearized version of the factorization problem (P*Q=35)
* this linearization can be automatically done by the parsers we provide
min: +1 x1 +2 x2 +4 x3;
+1 x1 +2 x2 +4 x3 >= 2;
+1 x4 +2 x5 +4 x6 >= 2;
+1 x7 +2 x8 +4 x9 +2 x10 +4 x11 +8 x12 +4 x13 +8 x14 +16 x15 = 35;
* new variables introduced to represent the products
+1 x7 -1 x1 -1 x4 >= -1;
-2 x7 +1 x1 +1 x4 >= 0;
+1 x8 -1 x1 -1 x5 >= -1;
-2 x8 +1 x1 +1 x5 >= 0;
+1 x9 -1 x1 -1 x6 >= -1;
-2 x9 +1 x1 +1 x6 >= 0;
+1 x10 -1 x2 -1 x4 >= -1;
-2 x10 +1 x2 +1 x4 >= 0;
+1 x11 -1 x2 -1 x5 >= -1;
-2 x11 +1 x2 +1 x5 >= 0;
+1 x12 -1 x2 -1 x6 >= -1;
-2 x12 +1 x2 +1 x6 >= 0;
+1 x13 -1 x3 -1 x4 >= -1;
-2 x13 +1 x3 +1 x4 >= 0;
+1 x14 -1 x3 -1 x5 >= -1;
-2 x14 +1 x3 +1 x5 >= 0;
+1 x15 -1 x3 -1 x6 >= -1;
-2 x15 +1 x3 +1 x6 >= 0;
|
* #variable= 6 #constraint= 3 #product= 9 sizeproduct= 18
*
* Factorization problem: find the smallest P such that P*Q=N
* P is a 3 bits number (x3 x2 x1)
* Q is a 3 bits number (x6 x5 x4)
* N=35
*
* minimize the value of P
min: +1 x1 +2 x2 +4 x3 ;
* P>=2 (to avoid trivial factorization)
+1 x1 +2 x2 +4 x3 >= 2 ;
* Q>=2 (to avoid trivial factorization)
+1 x4 +2 x5 +4 x6 >= 2 ;
* P*Q=N
+1 x1 x4 +2 x1 x5 +4 x1 x6 +2 x2 x4 +4 x2 x5 +8 x2 x6 +4 x3 x4 +8 x3 x5 +16 x3 x6 = 35;
|
The syntax of the input file format can be described by a simple BNF
grammar (see http://en.wikipedia.org/wiki/Backus-Naur_form).
<formula> is the start symbol of this grammar.
<formula>::= <sequence_of_comments>
[<objective>]
<sequence_of_comments_or_constraints>
<sequence_of_comments>::= <comment> [<sequence_of_comments>]
<comment>::= "*" <any_sequence_of_characters_other_than_EOL> <EOL>
<sequence_of_comments_or_constraints>::=<comment_or_constraint> [<sequence_of_comments_or_constraints>]
<comment_or_constraint>::=<comment>|<constraint>
<objective>::= "min:" <zeroOrMoreSpace> <sum> ";"
<constraint>::= <sum> <relational_operator> <zeroOrMoreSpace> <integer> <zeroOrMoreSpace> ";"
<sum>::= <weightedterm> | <weightedterm> <sum>
<weightedterm>::= <integer> <oneOrMoreSpace> <term> <oneOrMoreSpace>
<integer>::= <unsigned_integer> | "+" <unsigned_integer> | "-" <unsigned_integer>
<unsigned_integer>::= <digit> | <digit><unsigned_integer>
<relational_operator>::= ">=" | "="
<variablename>::= "x" <unsigned_integer>
<oneOrMoreSpace>::= " " [<oneOrMoreSpace>]
<zeroOrMoreSpace>::= [" " <zeroOrMoreSpace>]
For linear pseudo-Boolean instances, <term> is defined as
<term>::=<variablename>
For non-linear instances, <term> is defined as
<term>::= <oneOrMoreLiterals>
<oneOrMoreLiterals>::= <literal> | <literal> <oneOrMoreSpace> <oneOrMoreLiterals>
<literal>::= <variablename> | "~"<variablename>
Some comments and details:
- A line starting with a '*' is a comment and can be ignored.
Comment lines are allowed anywhere in the file.
- As a hint to perform memory allocation, the first line of a
linear instance will be a comment containing the word "#variable="
followed by a
space and the number of variables in the file, then a space and the
word "#constraint=" followed by a space and the number of constraints
in the file. The space between the word and the number is mandatory to
make parsing trivial. This information is only provided as a commodity
for solvers which include a very limited parser. High quality provers
are
encouraged to ignore this information as it may not be accurate outside
the evaluation environment (e.g. when a user creates a file by hand).
- For a non-linear instance, the first line will be a comment
containing the word "#variable=" followed by a
space and the number of variables in the file, then a space and the
word "#constraint=" followed by a space and the number of constraints
in the file then a space, the word "#product=" and a space, the number
of different products of variables present in the file, then a space
then the word "sizeproduct=" followed by a space and the total number
of literals which appear in different products. These two last
informations allow the parsers to compute the total number of linear
constraints that will be passed to the solver when the parser is asked
to linearize the formula. The keyword "#product=" also clearly
indicates that this is a non-linear instance.
- Each non comment line must end with a semicolon ';'
- The first non comment line may be an objective function to
minimize. It starts with the word "min:" followed by the linear
function to minimize and terminated by a semicolon. No other objective
function can be found after this first non comment line.
- A constraint is written on a single line and is terminated by a
semicolon.
- A Boolean variable (atom) is named by a lowercase 'x' followed by
a strictly positive integer number. The integer number can be
considered as a identifier of the variable. This integer identifier is
strictly less than 232. Therefore, a solver can input a
variable name by reading a character (to skip the 'x') and then an unsigned
long int.
- Inside the evaluation environment, variable names are guaranteed
to range from "x1" to "xN" where N is the total number of variables in
the instance (as given on the first line of the file). Each variable
between x1 and xN will occur in at least one constraint or the
objective function. High quality provers are encouraged to avoid
relying on this assumption as it may not hold outside the evaluation
environment.
- Inside the evaluation environment, variables that appear inside a
product are guaranteed to be ordered from the lowest to the greatest
index. High quality provers are encouraged to avoid
relying on this assumption as it may not hold outside the evaluation
environment.
- Inside the evaluation environment, a product term will never
contain a single negative literal (this literal ~L will be
replaced by 1-L during the normalization process)
- Inside the evaluation environment, each variable present in the
objective function will occur in at least one constraint. High quality
provers are encouraged to avoid relying on this assumption as it may
not hold outside the evaluation environment.
- Each variable name must be followed by a space
- The negation of an atom A will not appear in a linear
pseudo-Boolean file (it will be translated to 1-A). However, in
non-linear pseudo-Boolean instances it can appear as ~A
- The weight of a variable may contain an arbitrary number of
digits. There must be no space between the sign of an integer and its
digits.
- Lines may be very long. Programmers should avoid reading a line
as a whole.
Notice that integers may be of arbitrary size in the
file. See here for a rationale.
The rules let us write a very simple parser and avoid some ambiguities
present in the original description of the OPB format. At the same
time, the format remains easily human readable and is mostly compatible
with
solvers using the OPB format.
Output Format
Solvers must output messages to the standard output and those messages
will be used to check the results. The output format is inspired by the
DIMACS output specification of the SAT competition and may be used to
manually check some results.
Messages
With the exception of the "o " line, there is no specific order in the
solvers output lines. However, all lines, according to its first char,
must belong to one of the four following categories:
- comments ("c " lines)
These lines start by the two characters: lower case c followed by a
space (ASCII code 32).
These lines are optional and may appear anywhere in the solver output.
They contain any information that authors want to
emphasize, such as #backtracks, #flips,... or internal cpu-time. They
are recorded by the evaluation environment for later viewing but are
otherwise ignored. At most one megabyte of solver output will be
recorded. So, if a solver is very verbose, some comments may be lost.
Submitters are advised to avoid outputing comment lines which may be
useful in an interactive environment but otherwise useless in a batch
environment. For example, outputing comment lines with the number of
constraints read so far only increases the size of the logs with no
benefit.
If a solver is really too verbose, the organizers will ask the
submitter to remove some comment lines.
- value of the objective function
("o " lines)
These lines start by the two characters: lower
case o followed by a space (ASCII code 32).
These lines are mandatory for
incomplete solvers. As far as complete solvers are concerned,
they are not strictly mandatory but solvers are strongly invited to
output
them.
These lines should be output only for optimisation instances. They will
be ignored for SAT/UNSAT instances.
Whenever the solver finds a solution with a better value of the
objective function, it is asked to output an "o " line with the current
value of the objective function. Therefore, an "o " line must contain
the lower case o followed by a space and then by an integer which
represents the better value of the objective function. The integer
output on this line must be the value of the objective function as
found in the instance file. "o " lines should be output as soon as the
solver finds a better solution and be ended by a standard Unix end of
line character ('\n'). Programmers are advised to flush immediately the
output stream.
Example:
The instance file contains an objective function min: 1 x1 +1 x2
-1 x3
Let f be this objective function found in the file.
The solver chooses to rewrite this function as f '=x1+x2+not(x3) to get
only positive weights. It must remember that f=f '-1 (since
-x=not(x)-1). When it finds a solution x1=true, x2=true, x3=false, it
must output "o 2" (f ' has value 3 with this assignment but f has value
2). If x1=false, x2=false and x3=true is a solution, the solver may
successively output
o 2
o 1
o -1
s OPTIMUM FOUND
v -x1 -x2 x3
The evaluation environment will automatically timestamp each of these
lines so that it is possible to know when the solver has found a better
solution and how good the solution was. The goal is to analyse the way
solvers progress toward the best solution. As an illustration, here is
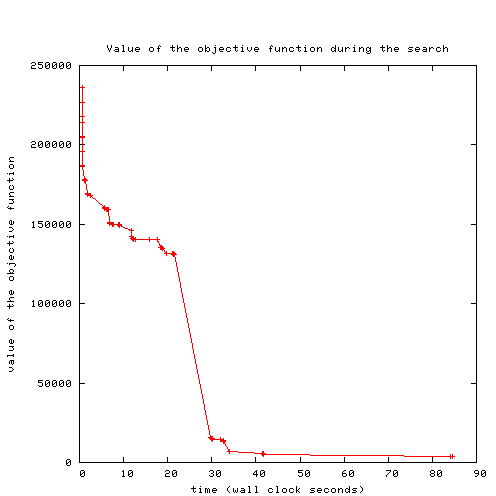
a sample of the output of a solver, with each line timestamped (first
column, expressed in seconds of wall clock time since the beginning of
the program).
0.00
c Time Limit set via TIMEOUT to 1800
0.51 c Initial problem consists of
6774 variables and 100 constraints.
0.55 c No problem reductions applied
in OPT. instance.
0.55 c preprocess
terminated. Elapsed time: 0.45
0.55 c After prepocess the problem
consists of 6774 variables and 100 constraints.
0.55 c Initial Lower Bound: 0
0.63 o 235947
0.63 o 226466
0.63 o 217758
0.75 o 186498
1.16 o 178319
2.42 o 168389
3.13 c Restart #1 #Var: 6774 LB: 0 @
3.03
4.89 c Restart #2 #Var: 6774 LB: 0 @
4.79
5.73 o 160358
6.44 o 159206
7.52 o 150077
9.09 o 149533
12.14 o 140853
17.74 o 140264
19.61 o 131636
29.81 o 15450
34.00 o 7066
41.66 o 5000
84.01 o 3905
84.01 c NEW SOLUTION FOUND: 3905 @ 83.873
84.61 s OPTIMUM FOUND
84.61 v -x1 -x2 -x3 x4 -x5 -x6 -x7 -x8 -x9
-x10 -x11 -x12 -x13 -x14 -x15 -x16 -x17 -x18 -x19 -x20 -x21 -x22 -x23
-x24 -x25 -x26 -x27 -x28
84.61 c Total time: 84.478 s
and here is the graph which can be generated from this data
- solution ("s " lines)
This line starts by the two characters: lower case s followed by a
space (ASCII code 32).
Only one such line is allowed.
It is mandatory.
This line gives the answer of the solver. It must be one of the
following answers:
- s SATISFIABLE
This line indicates that the solver has found a model of
the formula, and in such a case, a "v " line is mandatory.
For decision problems, this line must be output when the solver has
found a solution.
For optimization problems, this line must be in the output when the
solver has found a solution
but it can not prove that this solution gives the best value of the
objective function.
- s OPTIMUM FOUND
this line must be in the output when the solver has found a model
and it can prove that no other solution will give a better value of the
objective function than the one obtained with this model.
Let v be the value of the objective obtained with the valuation output
by the solver. Giving this result is a commitment that the formula
extended with the constraint objective<v is unsatisfiable.
This answer must not be used for instances which do not contain an
objective function.
- s UNSATISFIABLE
this line must be output when the solver can prove that the formula has
no solution.
- s UNKNOWN
this line must be output in any other case, i.e. when the
solver is not able to tell anything about the formula.
It is of uttermost importance to respect the exact spelling of these
answers. Any mistake in the writing of these lines will cause the
answer to be disregarded.
Solvers are not required to provide any specific exit code
corresponding to their answer.
If the solver does not output a solution line, or if
the
solution line is misspelled, then UNKNOWN will be assumed.
- values ("v " lines)
This line starts by the two characters: lower case v followed by a
space (ASCII code 32).
More than one "v " line is allowed but the evaluation environment will
act as if their content was merged.
It is mandatory when the instance is satisfiable.
If the solver finds a solution (it outputs "s SATISFIABLE" or "s
OPTIMUM FOUND"), it must provide a model (or an implicant) of the
instance that will be used to check the correctness of the answer,
i.e., it must provide a list of non-contradictory literals which, when
interpreted to true, makes every constraint of the input formula true.
When optimization is considered, this set of literals should provide
a model such that the value of the objective funtion corresponds
to the best one that the solver was able to find. The negation of a
literal is denoted by a minus sign immediately followed by the
identifier of the variable. The solution line MUST define the value of
EACH VARIABLE. The order of literals does not matter.
Arbitrary white space characters, including ordinary white spaces,
newline and tabulation characters, are allowed between the literals, as
long as each line containing the literals is a values line,
i.e. it begins with the two chars "v ".
The values lines should only appear with SATISFIABLE
instance (including instances for which an OPTIMUM was FOUND).
Values lines must be terminated by a Line Feed character (the
usual Unix line terminator '\n'. A "v " line which does not end with
that terminator will be ignored because it will be considered that the
solver was interrupted before it could output a complete solution.
For instance, the following outputs are valid for the instances
given in example:
mycomputer:~$ ./mysolver myinstance-sat
c mysolver 6.55957 starting with TIMEOUT fixed to 1000s
c Trying to guess a solution...
s SATISFIABLE
v x1 x2 -x5 x4 -x3
c Done (mycputime is 234s).
mycomputer:~$ ./mysolver myinstance-unsat
c mysolver 6.55957 starting with TIMEOUT fixed to 1000s
c Trying to guess a solution...
c Contradiction found!
s UNSATISFIABLE
c Done (mycputime is 2s).
Note that we do not require a proof for unsatisfiability.
A solver is declared to give a wrong answer in the following cases:
- It outputs UNSATISFIABLE for an instance which can be proved to
be satisfiable.
- It outputs SATISFIABLE or OPTIMUM FOUND, but provides an
assignment which does not satisfy each constraint. The only exception
is when the solver outputs an incomplete "v " line (which does not
end by '\n') in which case it is assumed that the solver was
interrupted before it could output the complete model and the answer
will be considered as UNKNOWN.
- It outputs OPTIMUM FOUND but there exists a model with a better
value of the objective function that the one obtained from the model
found.
When a solver provides even one single
wrong answer in a given category of benchmarks, the solver's results in
that category will be excluded from the final evaluation results
because they cannot be trusted. Exceptionally, the organizers
may decide to present separately the results of such a solver but only
if it obtained particularly good results and if a detailed explanation
of the problem as well as a solution is provided by the submitters.
A solver which ends without giving any solution, or just crashes for
some reason (internal bugs...), is simply considered as giving an
UNKNOWN result. It is buggy, but not incorrect.